Geometry: 110

111.    

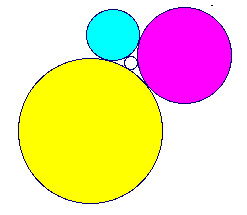
Geometry required. The three colored circles in the diagram above have radii of 1, 2, and 3, and each are tangent to the other two. A fourth interior circle is tangent to all three colored circles. What is the radius of the interior circle? For extra credit what is the radius of the exterior circle (not pictured) that is tangent to the three colored circles?

The following solution and diagrams are courtesy of James Sutton.

The triangle marked by the centers of the three outer circles conveniently forms a right triangle with sides 3, 4, and 5 (3² + 4² = 5²) as seen by the diagram below.

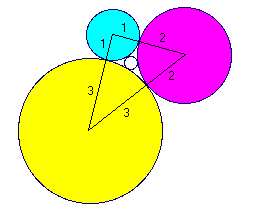
Next draw segments from the center of the interior circle and perpendicular to the outer triangle sides of length 3 and 4.

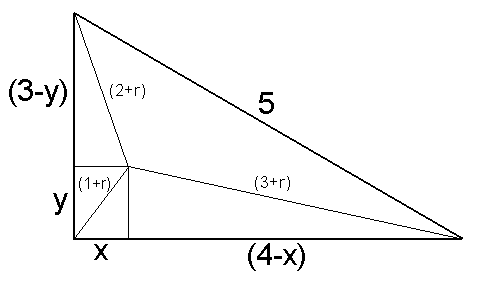
There are four right triangles in this picture, two of which are the same. Using the pythagorean formula we know:

(1): x² + y² = (1+r)²
(2): x² + (3-y)² = (r+2)²
(3): y² + (4-x)² = (r+3)²

Combining equations (1) and (2) we get y=(3-r)/3
Combining equations (1) and (3) we get x=(2-r)/2

Substituting these values for x and y back into equation 1 we get:

((2-r)/2)² + ((3-r)/3)² = r² + 2r + 1

This leads to...

23*r² + 132r - 36 = 0

Putting this through the quadratic formula we get r=6/23, -6

So the interior circle has radius 6/23 and the outer circle has radius 6.

--------------------------------------------------------------------------------------