Geometry : 119

106.   

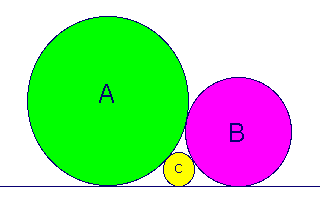
Geometry required. The three circles in the diagram above all are tangent to the line in the picture. The radius of circle A is a, of circle B is b, and of circle C is c. All three circles are tangent to each other. What is c as a function of a and b?

Problem 106 Solution

Define u as the center of circle A, v the center of circle B, and w the center of circle C. Define x as the point tangent to circle A and the line, y as the point tangent to circle B and the line, and z as the point tangent to circle C and the line.

uwzx forms a trapazoid with sides of length a,a+c,c,2*sqr(ac) per the pythagorean formula. Likewise the bottom of trapazoid vyzw is 2*sqr(bc) and the bottom of trapazoid uvyx is 2*sqr(ab).

The sum of the bottoms of trapazoids uwzx and vyzw is equal to the bottom of trapazoid uvyx:

2*sqr(ac)+2*sqr(bc)=2*sqr(ab)

sqr(ac)+sqr(bc)=sqr(ab)

sqr(c)*(sqr(a)+sqr(b))=sqr(ab)

sqr(c)=sqr(ab)/(sqr(a)+sqr(b))

c=ab/(a+2*sqr(ab)+b)

Note: Steve Schaefer points out the following general relationship a^-1/2 = b^-1/2 + c^-1/2